Mediation analysis presentation

Learn what mediation analysis is and how to run the analysis in R

1 Mediation analysis

1.1 Definition

Mediation analysis tests a hypothetical causal chain where one variable X affects a second variable M and, in turn, that variable affects a third variable Y. Mediators describe the how or why of a relationship between two other variables. Mediators describe the process through which an effect occurs. This is also sometimes called an indirect effect.

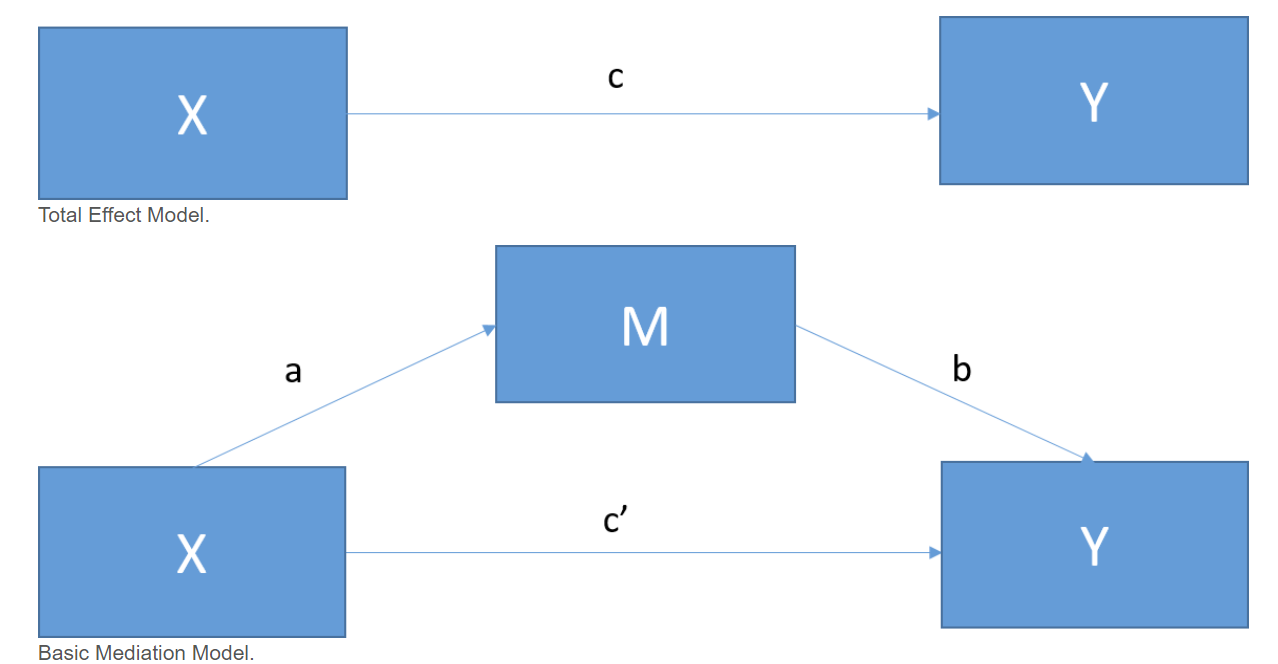
1.2 Types of effect

Total effect of X on Y: c = c’ + ab
Indirect effect of X on Y: ab
Direct effect of X on Y after controlling for M: c’ = c - ab

The original figure can be found here

2 Total mediation versus partial mediation

2.1 Understanding the different mediation effects

Partial mediation occurs when the effect of X on Y decreases by a nontrivial amount (the actual amount is up for debate) with M in the model.

One speaks of total mediation when the direct effect disappears as a result of mediation: c != 0, and thus ab = c.

One speaks of partial mediation when the direct effect does not disappear as a result of the mediation, but a residue remains: c!= 0 (i.e. if ab != c).

In the social science context, mediations are mostly partial, because one process rarely explains the full influence of X on Y.

3 Why consider ab instead of c-c’?

The difference method (c-c’) originally assumed that c must be significant (that is, that the X must have a total effect on the Y, which is to be explained by mediation).

However, mediation can also exist if c = 0. This is possible because there may be several significant mediator effects that cancel each other out (but not all may have been measured).

The targeted examination of ab thus provides a more precise picture of individual significant mediation processes, even if there is no total effect.

3.1 Example when c and c’ cancel each other

Example: participation in social demonstrations (X) and satisfaction with government (Y) mediated by media consumption (M).

Presumably, we have the following relations:

negative direct effect of X on Y: more participation in (anti-government) demonstrations suggests less satisfaction with government
positive direct effect of X on M: more participation in demonstrations suggests more media consumption
positive direct effect of M on Y: more media consumption suggests more satisfaction with government

Thus, we obtain:

a positive indirect effect
a very small total effect of X on Y because the direct and indirect effects will tend to cancel each other out

4 Ways to conduct mediation analysis

4.1 Three different methods

Baron & Kenny’s (1986) 4-step indirect effect method
“mediation” package (Tingley et al., 2014)
“lavaan” is the R package that handles measurement and analysis models most easily. For the calculation, the model formula and the data are passed to the sem() function.

Typical questions are:

Whether there is a total effect of the independent variables on the dependent variable?
Whether there is a significant mediation effect?
- If so, is there partial or total mediation?

4.2 Method with 4-steps from Baron & Kenny

estimate the relationship between X on Y (c must be significantly different from 0)
estimate the relationship between X on M (a must be significantly different from 0)
estimate the relationship between M on Y controlling for X (b must be significantly different from 0)
estimate the relationship between Y on X controlling for M (should be non-significant and nearly 0)

In general, complete mediation implies that these step 1-2-3-4 (in the 4-steps from Baron & Kenny) be met. However, in practice, some researchers also consider that the essential steps in establishing mediation are steps 2 (X on M) and 3 (Z on Y, controlling for X).

Furthermore, if c′ had the opposite sign to that of ab, then there would still be mediation (even if step 1 could not be met).

4.3 Sobel test

It is generally recommended to perform a single test of ab (rather than two separated tests of a and b). The test was first proposed by Sobel (1982).

The test of the indirect effect is given by dividing ab by the standard error estimate of ab. The ratio is treated as a Z test:

\[ z = \frac{ab}{\sqrt{b^2*s^2_{a} + a^2*s^2_{b}}} \]

If a z-score is larger than 1.96 in absolute value, the mediation effect is significant at the .05 level.

The Sobel test is easy to conduct but presumes that a and b are independent (which may not always be true). Furthermore, it assumes that ab is normally distributed (which might not work well for small sample sizes).

4.4 R mediation package

This package uses the more recent bootstrapping method of Preacher & Hayes (2004) to address the power limitations of the Sobel test. This method computes the point estimate of the indirect effect (ab) over a large number of random sample (typically 1000) so it does not assume that the data are normally distributed and is especially more suitable for small sample sizes than the Barron & Kenny method.

This method includes 2-steps:

estimate the relationship between X on M
estimate the relationship between X on Y controlling for M

4.5 Bootstrap

One solution to the drawback of the Sobel test is to use the bootstrap method (see Bollen & Stine, 1990). This method has no distribution assumption on the indirect effect ab, but rather approximates the distribution of ab using its bootstrap distribution.

Using the original data set (Sample size = n) as the population, the model draws a bootstrap sample of n individuals with paired (Y, X, M) scores randomly from the data set with replacement. From the bootstrap sample, estimate ab based on a set of regression models. The steps are repeated for a total of N times (N=number of bootstraps).

5 Example in R

5.1 Example: news attention as mediator

For example, citizens’ media diet (e.g., attention to political news) could mediate the effect of trust in politicians (e.g., trust in national parties) on the frequency of political participation to popular votes (over the 10 last votes).

We will be using the Selects Swiss Panel Election Study 2019 and the following variables:

Y: participation over the last 10 popular votes: W1_f12500
X: trust in politicians: W3_f12800c (in W3)
M: media diet (in W2): W2_f13400a-f

The regression equations go as:

\[ Y_i = \beta_0 + \beta_1*trust_i + \beta_2*media_i + \epsilon_i = c' + b \] \[ M_i = \beta_0 + \beta_1*trust_i + \epsilon_i = a \] \[ Y_i = \beta_0 + \beta_1*trust_i + \epsilon_i = c = c' + ab \]

5.2 Prepare the data

db <- foreign::read.spss(file=paste0(getwd(),
                "/data/1184_Selects2019_Panel_Data_v4.0.sav"), 
                use.value.labels = T, 
                to.data.frame = T)
sel <- db |>
  dplyr::select(W3_f11100,W1_f12500,W3_f12800c,
                W2_f13400a,W2_f13400b,W2_f13400c,
                W2_f13400d,W2_f13400e,W2_f13400f) |>
  stats::na.omit() |>
  dplyr::rename("particip"="W3_f11100",
                "particip10v"="W1_f12500",
                "party_trust"="W3_f12800c",
                "tv"="W2_f13400a",
                "newsp"="W2_f13400b",
                "freen"="W2_f13400c",
                "socmed"="W2_f13400d",
                "online"="W2_f13400e",
                "radio"="W2_f13400f")

5.3 Recoding and creation of media use score

# recode participation over 10 votes
sel$particip10v <- as.character(sel$particip10v)
sel$particip10v[sel$particip10v=="10 votes out of 10"] <- "10"
sel$particip10v[sel$particip10v=="0 votes out of 10"] <- "0"
sel$particip10v <- as.numeric(sel$particip10v)
# trust as numeric
sel$party_trust <- as.character(sel$party_trust)
sel$party_trust[sel$party_trust=="Full trust"] <- "10"
sel$party_trust[sel$party_trust=="No trust"] <- "0"
sel$party_trust <- as.numeric(sel$party_trust)
# trust as binary
sel$party_trust_b <- ifelse(sel$party_trust>=6, "yes","no")
# reverse scale for media attention
sel$tv <- (as.numeric(sel$tv)-4)*(-1)
sel$newsp <- (as.numeric(sel$newsp)-4)*(-1)
sel$freen <- (as.numeric(sel$freen)-4)*(-1)
sel$socmed <- (as.numeric(sel$socmed)-4)*(-1)
sel$online <- (as.numeric(sel$online)-4)*(-1)
sel$radio <- (as.numeric(sel$radio)-4)*(-1)
sel$medatt <- (sel$tv+sel$newsp+sel$freen+sel$socmed+sel$online+sel$radio)/6

5.4 “mediation” package: interpretation and bootstrap

fitM <- lm(medatt ~ party_trust, # M ~ X
           data=sel) 
fitY <- lm(particip10v ~ party_trust + medatt, # Y ~ M + X
           data=sel) 
fitMed <- mediation::mediate(fitM, fitY, 
                             # boot=TRUE, 
                             # sims=999,
                             treat="party_trust", 
                             mediator="medatt")
summary(fitMed)


Causal Mediation Analysis 

Quasi-Bayesian Confidence Intervals

               Estimate 95% CI Lower 95% CI Upper p-value    
ACME            0.01493      0.00489         0.02   0.002 ** 
ADE             0.08427      0.04455         0.12  <2e-16 ***
Total Effect    0.09920      0.05758         0.14  <2e-16 ***
Prop. Mediated  0.15164      0.05274         0.28   0.002 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Sample Size Used: 3937 


Simulations: 1000

ACME: Average Causal Mediation Effects (here: significant effect of media attention on the relationship between trust and participation)
ADE: Average Direct Effects (here: significant direct effect of trust)
Total effect: combined indirect and direct effects (here: significant)
Prop. Mediated: ratio of indirect and total effects (ACME divided by Total Effect)

5.5 “lavaan” package

# let's add the indirect and total effects explicitly in the model
modell.tot = "
  particip10v ~ cp*party_trust ## direct effect (c'-path)
  medatt ~ a*party_trust ## a-path
  particip10v ~ b*medatt ## b-path
  ab := a*b ## indirect effect (ab)
  total := cp+a*b ## total effect 
"
fit.tot = lavaan::sem(modell.tot, data=sel)
lavaan::parameterestimates(fit.tot, standardized = T)[c(1:5,8)]

          lhs op         rhs label   est pvalue
1 particip10v  ~ party_trust    cp 0.085  0.000
2      medatt  ~ party_trust     a 0.014  0.001
3 particip10v  ~      medatt     b 1.107  0.000
4 particip10v ~~ particip10v       6.340  0.000
5      medatt ~~      medatt       0.263  0.000
6 party_trust ~~ party_trust       3.712     NA
7          ab :=         a*b    ab 0.015  0.002
8       total :=      cp+a*b total 0.100  0.000

lavaan::inspect(fit.tot,"r2")

particip10v      medatt 
      0.054       0.003

The indirect effect (ab) of the independent variable via the mediator on the dependent variable is significant and positive.

The direct effect (cp) is also significant. Since the indirect effect (ab) is significant at the same time, there is no complete mediation.

The link between the trust (X) and participation (Y) is partially conveyed through the media diet (M).

5.6 Further interpretation

lavaan::parameterestimates(fit.tot, standardized = T)[c(1:5,8)]

          lhs op         rhs label   est pvalue
1 particip10v  ~ party_trust    cp 0.085  0.000
2      medatt  ~ party_trust     a 0.014  0.001
3 particip10v  ~      medatt     b 1.107  0.000
4 particip10v ~~ particip10v       6.340  0.000
5      medatt ~~      medatt       0.263  0.000
6 party_trust ~~ party_trust       3.712     NA
7          ab :=         a*b    ab 0.015  0.002
8       total :=      cp+a*b total 0.100  0.000

a-path: every 1-unit increase in trust is associated with an a = 0.014 increase in media attention.
b-path: adjusting for trust, every 1-unit increase in media attention was associated with participation b = 1.107.
for every a = 0.014 unit increase in the association between trust and media attention, there is an ab = 0.015 increase in participation. So, increase in participation is associated with increase in trust indirectly through media attention.