Structural equation modelling (SEM) presentation

Learn what SEM is and how to run the analysis in R

1 Structural equation model (SEM)

1.1 Definition

SEM enable us to answer questions such as:

• Do my data confirm my previously made hypothetical assumptions about the “causal” structure between variables?

Simply speaking, SEM are a combination of CFA and path analysis.

SEM include two sets of models:

• the measurement model
• the structural model

1.2 Logic of SEM and similarity with CFA

SEM are hypothesis-testing methods.

Previously theoretically deduced considerations on relationships between variables are tested using empirical data.

It is thus determined in advance which variables may/should be related and which should not (similar to CFA).

As with the CFA, it is a comparison of covariance matrices that are checked as a whole:

• empirical variance-covariance matrix (= actual correlations between all examined variables in the data)
• model-theoretical variance-covariance matrix (= expected relationships between all variables examined)

SEM allow the testing of entire hypotheses systems in one model.

1.3 Comparison to normal regression

Linear regression models “unrealistically” assumes that constructs are perfectly measured, thus confusing measurement error with statistical error (e.g. unexplained variance).

SEM with latent variables allow the measurement error to be extracted from the statistical error.

Therefore, SEM come with potentially more exact estimation of the significance and strength of the connections between latent variables.

1.4 Path models

A path model is a special case of a SEM in which the structural model is present but the measurement model is omitted (exclusively manifest constructs in the structural model).

Path models can also be calculated as SEM in the covariance analysis approach (including model quality measures, etc.), but for better differentiation they are not called SEM but path models.

1.5 Construct validity, model fit, and explanation of relationships

SEM seeks to find a balance between maximizing the variance between constructs while ensuring the model remains parsimonious and generalizable.

Maximizing the sum of squares between constructs can be useful in several respects:

• Reliability and validity assessment: higher variance suggests that the latent variable accounts for a larger proportion of the variation in the observed indicators, which contributes to the construct’s reliability and validity.
• Model fit and explanation of relationships: a model that explains a higher proportion of the variance in the observed variables tends to fit the data better.
• Precision in estimation (robustness of conclusions): higher variance between constructs often results in more precise estimates of the relationships among constructs.

2 Recap and new concepts

2.1 Concepts

Recap:

• Observed variable: Exists in data
• Indicator: Observed (exogenous or endogenous)
• Latent variable: Constructed in model
• Factor: Latent (exogenous or endogenous)
• Measurement model: Links observed and latent variables
• Loading: Path between indicator and factor
• Regression model: Path between exogenous and endogenous variables

New:

• Exogenous: Independent that explains endogenous (observed or latent) -> predictor
• Endogenous: Dependent that has a causal path leading to it (observed or latent) -> response

2.2 Latent and manifest variables in SEM

In the structural model, the (“causal”) relationships between different variables are formulated (directed relationships!).

These variables can be both latent (= hypothetical, not directly observable) and manifest (= directly observable) constructs.

Latent variables are specified in the measurement model (like CFA) and are estimated in such a way that they best represent their respective manifest indicators (items).

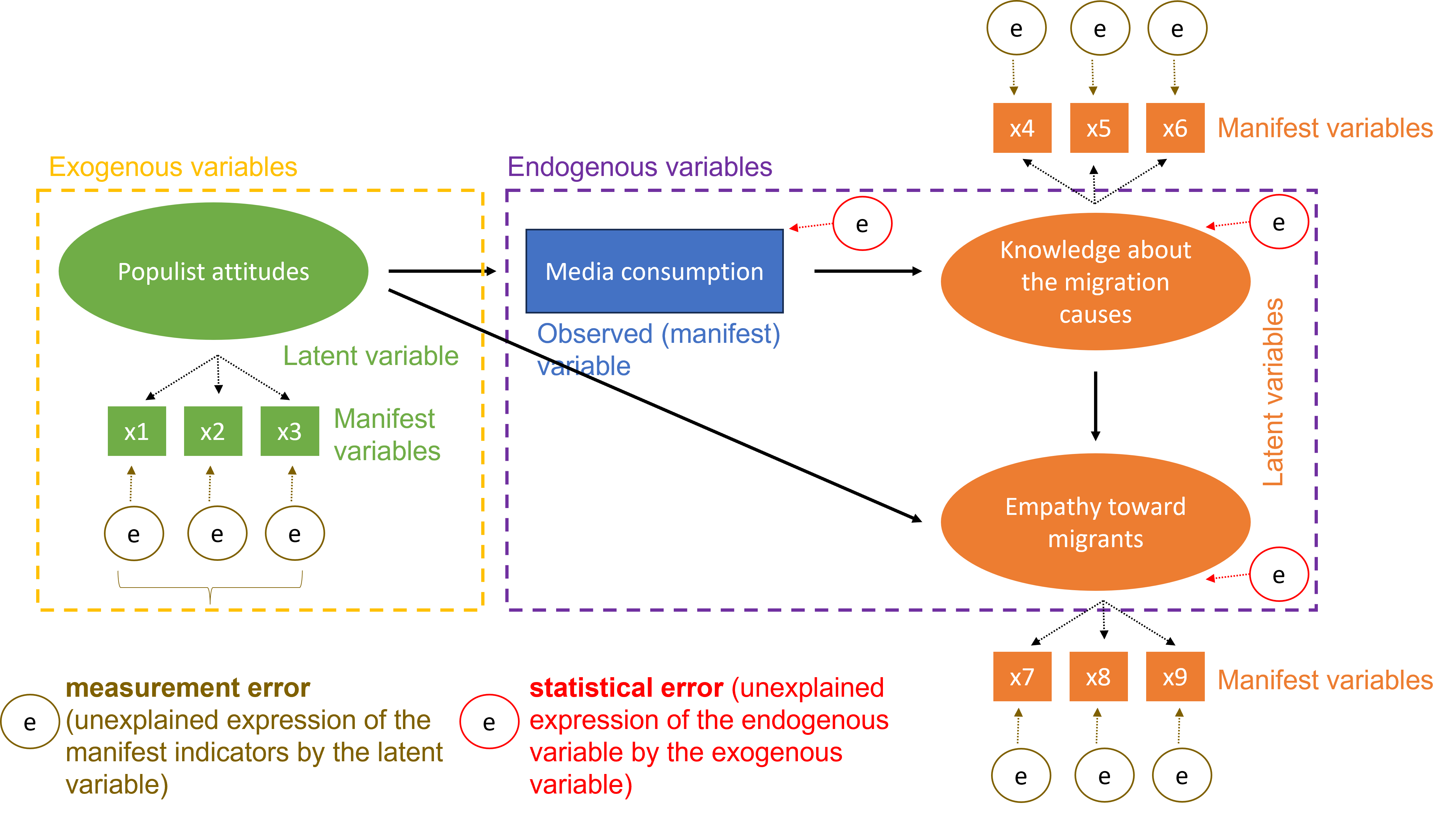
3 Statistical error versus measurement error

3.1 Two types of errors

SEM with latent variables allow the distinction between:

• statistical error in estimating the “causal” influences of the exogenous on the endogenous variables (unexplained expression of the endogenous variable by the exogenous variable)
• measurement error of the variable (unexplained expression of the manifest indicators by the latent variable).

3.2 Graphical representation

4 Prerequisites

4.1 Mathematical prerequisites

• Rule of thumb: sample size K at least 200 (also K - q > 50, where K is the sample size and q is the number of free parameters to be estimated)
• If only latent variables in the structural model:
  • Prerequisites as for CFA
  • Reflective measurement model
  • Interval-scaled and reasonably normally distributed manifest indicator variables
• If partially latent and partially manifest constructs in the structural model:
  • SEM can handle a mixture of manifest and latent constructs in the structural model very well
  • Structural equation system must be identifiable, i.e. the equation system must be mathematically solvable (similar to CFA)

4.2 Theoretical prerequisites

• Theoretically secured hypotheses about the connection between constructs in the SEM
  • Especially with cross-sectional data: theoretically reasonable deduced “causal direction” (which constructs are exogenous, which endogenous?)
• Adhere to the confirmatory character of the analysis or, if this is not done, then deal with it transparently
  • Strictly confirmatory testing: If we proceeded strictly confirmatory, we could only specify one model and accept or reject it with a test (hypothesis testing).
  • Alternative models testing: Testing different plausible theories against each other
  • Generating adaptation of the model until the data “fit”

5 Identification

5.1 Identification of the structure

The identification of the model structure consists of two “tasks”:

• Establishing a metric for the latent constructs.
• Checking whether there is enough information to estimate the model.

Both steps influence the number of degrees of freedom of the model (model degrees of freedom). This aspect also relates to the complexity of the model.

5.2 Establishing metric

The latent variables and error variables to be estimated initially have no metric.

In order to be able to interpret the variable later, a scale must be assigned:

• choose a reference variable and fix the factor loading to 1.
• all relationships between the measurement error terms to be estimated and the measured indicator variables are fixed at 1.

5.3 Checking model information

If n manifest variables are collected as part of a project, empirical variances and covariances can be calculated from these variables:

\[ p = \frac{n(n+1)}{2} \]

where \(p\) corresponds to the number of non-redundant values in the variance-covariance matrix. It thus corresponds to the available “information” that we use as the basis for calculating all free parameters of our model.

The difference between the available empirical information (\(p\)) and the number of (free) parameters to be estimated (\(q\)) gives the degrees of freedom of the model (\(df_M\)).

\[ df_M = p - q \]

5.4 Empirically available information (recap)

If the empirically available information is the same as the number of parameters to be estimated, the number of model degrees of freedom corresponds to zero.

The number of model parameters to be estimated must be fewer than (or equal to) the number of empirical information given; otherwise a model is not identified (i.e., not solvable).

The degrees of freedom of the model must be >=0 for a specified model to be considered identified.

6 Analytical steps for SEM

6.1 Four main steps

• Model Specification: defines hypothetical relationships
• Model Identification:
  • Over identified - more knowns than free parameters
  • Just-identified - the number of unknowns equals the number of free parameters
  • Under-identified - the number of unknowns is greater than the number of parameters (model coefficients cannot be estimated)
• Model Evaluation: goodness of fit (i.e. Chi-square, Akaike Information Criterion, Comparative Fit Index)
• Model Modification: post hoc model modification

6.2 Chi-square test

The Chi-Square test poses that:

• H0: empirical covariance matrix is equal to the model-theoretical covariance matrix
• H1: empirical covariance matrix is not equal to the model-theoretical covariance matrix

The smaller the difference between the two matrices, the smaller the chi-square value. So, the smaller the chi-square, the better. The test should not turn out to be significant, since equality between the empirical and model-theoretical variance-covariance matrix is desirable.

6.3 RMSEA (Root Mean Squared Error of Approximation)

RMSEA uses inferential statistics to check whether a model can approximate reality well (approximation test). It is therefore not about the absolute correctness of the model, as with the Chi-Square test, but about evaluating the best possible approximation.

Recommendations:

• RMSEA < .05 good fit
• RMSEA < .08 acceptable fit

6.4 SRMR (Standardized Root Mean Squared Residual)

Usually there is a discrepancy between the empirical and model-theoretical covariance matrix. Therefore, descriptive measures of discrepancy are often used. These give an answer to the question of whether an existing discrepancy can be neglected and also includes the model complexity. If the empirical and model-theoretical covariance matrix are completely identical, this measure assumes a value of zero.

Recommendations:

• SRMR < .05 good fit
• SRMR < .10 acceptable fit

6.5 Individual components

Have the individual components of the SEM (entire measurement model AND structural model) also been identified?

For structural models, this depends heavily on the structure:

• Recursive models (= models without repercussions between endogenous variables, i.e. directed models) are always identified
• Non-recursive models (= models with repercussions between endogenous variables, i.e. undirected models) are difficult to determine by hand, you should leave that to the statistics program

6.6 Critics to SEM

In relation to causality:

• The researcher decides (often) what are exogenous and what are endogenous variables.
• Directions of impact could be directed in the opposite direction as long as the method of data collection is cross-sectional.
• Causal evidence using SEM is only possible with panel data or in an experiment (and then not mandatory for all paths of the structural model).

In relation to theory:

• SEM are too often not tested for confirmation, but adjusted until the model fit is “good”, without this being reported transparently.
• The more paths between variables are freely estimated in the structural model, the less an SEM test theoretical ideas.

7 Example in R

7.1 Autoregressive model

Let’s imagine we have three variables to measure trust in politicians:

• politicians’ responsiveness (item “most politicians do not care about the people”)
• politicians’ corruption (item “most politicians care only about the interests of the rich and powerful”)
• politicians’ trustworthiness (item “most politicians are trustworthy”)

We have data on these variables before and after the election.

7.2 Problem statement

Assume we want to test whether trust in politicians before election can predict trust in politicians after election. Then the SEM model in the figure below can be used.

Note that we allow the factor in time 1 to predict the factor at time 2. In addition, we allow the uniqueness factors for each observed variable to be correlated.

7.3 Prepare the data

# load data
library(foreign)
db <- read.spss(file=paste0(getwd(),
                "/data/1184_Selects2019_Panel_Data_v4.0.sav"), 
                use.value.labels = F, 
                to.data.frame = T)
sel <- db |>
  dplyr::select(W3_Q04c,W4_Q04c,
                W3_Q04b,W4_Q04b,
                W3_Q04g,W4_Q04g) |>
  stats::na.omit() |>
  dplyr::rename("polit_trustworthy_1"="W3_Q04c",
                "polit_trustworthy_2"="W4_Q04c",
                "polit_carepeople_1"="W3_Q04b",
                "polit_carepeople_2"="W4_Q04b",
                "polit_rich_1"="W3_Q04g",
                "polit_rich_2"="W4_Q04g") 
for(i in 1:6){sel[,i] <- (as.numeric(sel[,i])-6)*(-1)}
for(i in 3:6){sel[,i] <- (sel[,i]-6)*(-1)}

7.4 Specifying the model

We can specify the model using the lavaan R package:

library(lavaan)
automodel <- '
 polit_trust_1_latent =~ polit_trustworthy_1 + polit_carepeople_1 + polit_rich_1
 polit_trust_2_latent =~ polit_trustworthy_2 + polit_carepeople_2 + polit_rich_2
 polit_trust_1_latent ~ polit_trust_2_latent
 polit_trustworthy_1 ~~ polit_trustworthy_2
 polit_carepeople_1 ~~ polit_carepeople_2
 polit_rich_1 ~~ polit_rich_2
'
auto.res <- sem(automodel, data=sel)
t <- summary(auto.res, fit=TRUE)

Reminder:

• “~” regression
• “=~” latent variable definition
• “~~” (co)variance

7.5 Interpretation

print(paste0(
  "Chi-squared ", 
  round(t[["test"]][["standard"]][["stat"]],3), 
  " with p-value ", 
  round(t[["test"]][["standard"]][["pvalue"]],3), 
  "; CFI: ", round(t[["fit"]][["cfi"]],3), 
  "; TFI: ", round(t[["fit"]][["tli"]],3), 
  "; RMSEA: ", round(t[["fit"]][["rmsea"]],3), 
  "; SRMR: ",round(t[["fit"]][["srmr"]],3)))

[1] "Chi-squared 4.706 with p-value 0.453; CFI: 1; TFI: 1; RMSEA: 0; SRMR: 0.007"

The chi-square value is 4.706 with 5 degrees of freedom. The p-value for chi-square test is almost 0.5. Thus, based on chi-square test, this is a good model (furthermore: CFI and TFI close to 1; RMSEA and SRMR about 0). Overall, this model is a fairly good model.

pe <- t[["pe"]]
pe <- as.data.frame(pe[!is.na(pe$pvalue),c(1,2,3,5,8)])
pe$est <- round(pe$est, 2); pe$pvalue <- round(pe$pvalue,2)
pe

                    lhs op                  rhs  est pvalue
2  polit_trust_1_latent =~   polit_carepeople_1 2.34   0.00
3  polit_trust_1_latent =~         polit_rich_1 2.20   0.00
5  polit_trust_2_latent =~   polit_carepeople_2 3.63   0.00
6  polit_trust_2_latent =~         polit_rich_2 3.39   0.00
7  polit_trust_1_latent  ~ polit_trust_2_latent 1.22   0.00
8   polit_trustworthy_1 ~~  polit_trustworthy_2 0.24   0.00
9    polit_carepeople_1 ~~   polit_carepeople_2 0.09   0.01
10         polit_rich_1 ~~         polit_rich_2 0.30   0.00
11  polit_trustworthy_1 ~~  polit_trustworthy_1 0.73   0.00
12   polit_carepeople_1 ~~   polit_carepeople_1 0.56   0.00
13         polit_rich_1 ~~         polit_rich_1 0.74   0.00
14  polit_trustworthy_2 ~~  polit_trustworthy_2 0.81   0.00
15   polit_carepeople_2 ~~   polit_carepeople_2 0.54   0.00
16         polit_rich_2 ~~         polit_rich_2 0.71   0.00
17 polit_trust_1_latent ~~ polit_trust_1_latent 0.03   0.00
18 polit_trust_2_latent ~~ polit_trust_2_latent 0.04   0.00

Trust before election seems to predict trust after election: those with higher trust in politicians before election tend to have higher trust level after election.