Show the code
# load the data
library(foreign)
db <- read.spss(file=paste0(getwd(),
"/data/protest.sav"),
use.value.labels = F,
to.data.frame = T)7 Moderation analysis
7.1 Moderation analysis
Moderation analysis allows us to test for the influence of a third variable, Z, on the relationship between variables X and Y. Rather than testing a causal link between these other variables, moderation tests for when or under what conditions an effect occurs.
For instance, we can start with a bivariate relationship between an input variable X (e.g. training) and an outcome variable Y (e.g. test score). We can hypothesize that there is a relationship between them. A moderator variable Z (e.g. gender) is a variable that alters the strength of the relationship between X and Y.
Moderators can strengthen, weaken, or reverse the nature of a relationship. Moderation can be tested by looking for significant interactions between the moderating variable (Z) and the independent variable (X).
Nota bene: Moderators (when) are conceptually different from mediators (how/why) but some variables may be a moderator or a mediator depending on your question.
7.2 Similarity with ANOVA
The moderation is an interaction and therefore comparable to the interaction in ANOVA. If X and moderator are dichotomous, the moderation corresponds to a 2x2 ANOVA.
However, a moderator moderates the causal relationship from X to Y. The scale level can be dichotomous, categorical or metric. Furthermore, a moderator must be causally independent of X.
Technically, moderations (interactions) are linked multiplicatively in the regression analysis: A x B.
Statistically, the moderator and X must always be considered “in isolation” (not just as moderation or interaction).
An illustration of the similarity between a simple moderation analysis and a 2x2 ANOVA can be found below (this example is taken from Igartua and Hayes (2021)):
7.3 The linear regression framework
Moderation analysis can be conducted by adding one (or multiple) interaction terms in a regression analysis. For example, if Z is a moderator for the relation between X and Y, we can fit a regression model:
\[ Y = \beta_{0} + \beta_{1}*X + \beta_{2}*Z + \beta_{3}*XZ + \epsilon \]
\[ Y = \beta_{0} + \beta_{2}*Z + (\beta_{1} + \beta_{3}*Z)*X + \epsilon \] Thus, if \(\beta_{3}\) is not equal to 0, the relationship between X and Y depends on the value of Z, which indicates a moderation effect.
If Z is a dichotomous/binary variable (e.g. gender) the above equation can be written as:
\[ \beta_{0} + \beta_{1}*X + \epsilon \] for male (Z=0)
\[ \beta_{0} + \beta_{2} + (\beta_{1} + \beta_{3})*X + \epsilon \] for female (Z=1)
7.4 Interpretation and centering
If X and/or moderator become significant, main effects are present. If the moderation term becomes significant, there is a moderation effect. The (possibly significant) influences of X and the moderator are then so-called “conditional” effects.
The value 0 usually has no meaningful meaning (e.g. in rating scales 1 to 5 there is no zero at all). Therefore, it is a good practice to centering means subtracting the overall mean from each value. The centering changes the interpretation decisively:
- if has the value 0, the moderator is moderately developed
- if has negative values, below-average characteristics are present
- if has positive values, above-average characteristics are present
The change in meaning must be taken into account in the interpretation:
- influence of the predictor on Y with an average expression of the moderator
- influence of the moderator on Y with an average expression of the predictor
7.5 Multicollinearity
The moderation term is formed with moderator and X. However, the moderator and X are also contained individually in the regression equation. This often leads to multicollinearity (i.e. low tolerances or high VIF values).
If moderator and X are centered, the symptoms of multicollinearity are superficially defused. However, the multicollinearity itself remains.
Reminder: Multicollinearity means that predictors are (too strongly) related to each other. Since the moderation term also consists of A (or B), it can easily correlate with A (or B).
7.6 Simple slopes
When the moderation effect becomes significant, it needs to be “illustrated” in order to make it interpretable. To do so, we can rely on simple slope analysis: comparison of the regression lines for low, medium and high levels of the moderator.
Typically, we use the mean value of the moderator, as well as the values + and - 1 SD are used, but theoretically any values can be considered.
7.7 Significance range according to Johnson & Neyman (only if moderation metric)
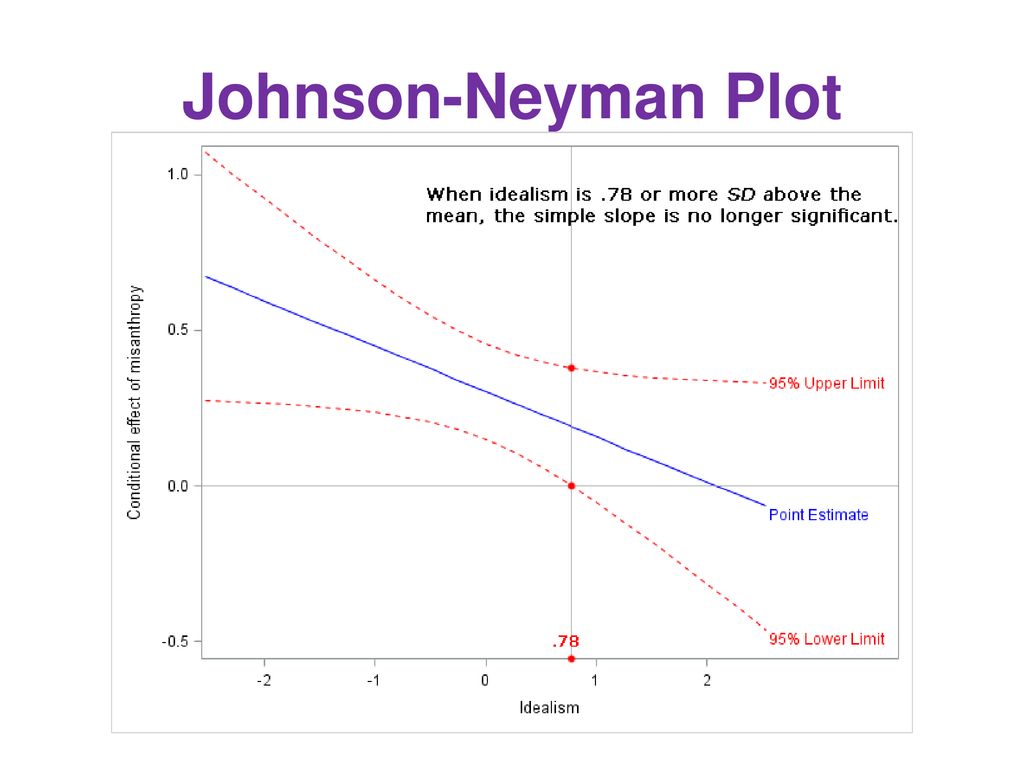
This method suggests to conduct comparison of the regression equation for many characteristics of the moderator to identify areas of significance.
It is more useful than simple slopes for metric moderators, since illustrations result in less loss of information in the moderator’s levels. The effect (b) of the X on Y is now illustrated in the diagram as a function of the moderator (not to be confused with a regression line!), as well as the confidence interval for this effect:
7.8 Steps in the analysis
A moderation analysis typically consists of the following steps:
- compute the interaction term X*Z
- fit a multiple regression model with X, Z, and XZ as predictors
- test whether the regression coefficient for XZ is significant or not
- interpret the moderation effect
- display the moderation effect graphically.
7.9 Important remarks: variable’s effect as a function of a moderator
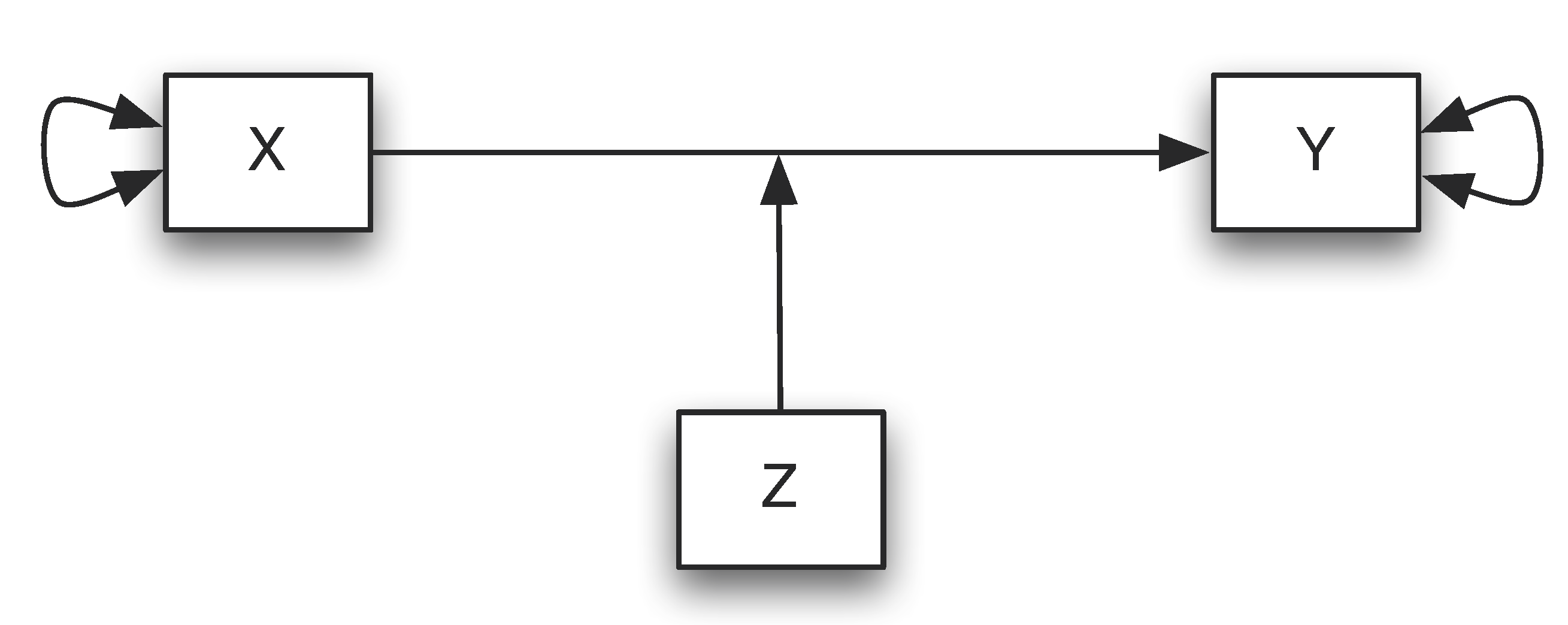
A conceptual representation of a simple moderation model with a single moderating variable Z modifying the relationship between X and Y.
Let’s assume that X and Z are either dichotomous or continuous and the outcome variable Y is a continuous dimension suitable for analysis with linear regression, we have the following equations:
\[ \hat{Y} = a + b_1*X + b_2*Z + b_3*XZ = a + (b_1+b_3*Z)X + b_2*Z\] In this representation, the weight for X is not a single number but, rather, a function of Z: \(b_1+b_3*Z\). The output is sometimes called the simple slope of X or the conditional effect of X. The coefficients \(b_1\) and \(b_2\) may or may not have a substantive interpretation, depending on how X and Z are coded or, in the case of dichotomous X and Z, what two numbers are used to represent the groups in the data.
Important remarks:
- It is never correct to interpret \(b_1\) as the effect of X on Y “controlling for” the effect of Z and XZ.
- It usually is not correct to interpret \(b_1\) as the “average effect” of X or the “main effect” of X (a term from analysis of variance that applies only when X and W are categorical)
- \(b_1\) can be the main effect of X from a 2X2 ANOVA if X and Z are coded appropriately.
- Similar arguments apply to the interpretation of \(b_2\).
Correct interpretation:
- \(b_1\) is the conditional effect of X on Y when Z = 0.
- \(b_1\) is the estimated difference in Y between two cases in the data that differ by one unit in X but have a value of 0 for Z.
- \(b_2\) is the conditional effect of Z on Y when X = 0.
- When X = 0, the conditional effect of Z reduces to \(b_2\).
- When Z = 0, X’s effect equals \(b_1\); when Z = 1, X’s effect equals \(b_1+b_3\); when Z = 2, X’s effect is \(b_1+2b_3\), and so forth.
7.10 Reporting the results
The following must be observed to report moderation analysis:
- always shows both (un)standardized effects
- in the case of a statistically significant interaction, the conditional effects (aka main effects) can no longer be interpreted unquestioningly
- in the case of a statistically significant interaction, the difference between several slopes in the model (e.g. those represented as simple slopes) is significant
7.11 Further resources
For a long time the PROCESS macro has been one of the best ways of testing moderations (interactions) when using SPSS. In December 2020, Hayes has released the PROCESS function for R.
To download Hayes’ PROCESS macro for R go here.
A tutorial about how to use the process() function in R can be found here.
7.12 In a nutshell
A moderation analysis is a regression analysis in which the dependent variable (Y) is predicted from an independent variable (X) and a moderator (Z) and the interaction of both (XZ).
X and Z should be centered prior to analysis. On the one hand, this simplifies the interpretation of the results and, on the other hand, helps against the effects of multicollinearity in the model.
If the interaction term becomes significant, there is moderation.
The moderation effect can be illustrated by simple slopes and significance areas according to Johnson-Neyman.
7.13 How it works in R?
See the lecture slides on moderation analysis:
You can also download the PDF of the slides here: 
7.14 Example from the literature
The following article relies explains moderation (and mediation) analysis with an illustrative example:
Igartua, J. J., & Hayes, A. F. (2021). Mediation, moderation, and conditional process analysis: Concepts, computations, and some common confusions. The Spanish Journal of Psychology, 24, e49. Available here.
Please reflect on the following questions:
- How is simple moderation analysis similar to a 2x2 ANOVA?
Solution
Simple moderation analysis is conceptually similar to a 2×2 ANOVA because both examine interactions between two variables to see whether the effect of one predictor on the outcome changes depending on another variable. In a 2×2 ANOVA, one tests whether the difference between group means on one factor varies across levels of another factor, which parallels how moderation tests whether the slope of a continuous predictor differs across levels of a moderator.
- What is the difference between “main effects” and “simple effects” models?
Solution
Main effects models focus on the independent influence of each variable while averaging over the levels of other predictors, assuming the effects are consistent across all conditions. In contrast, simple effects models break down the interaction by examining how one predictor affects the outcome at specific values or levels of the moderator, providing a more detailed understanding of where and how the interaction occurs.
- What is the advantage of using Johnson-Neyman technique to illustrate conditional effects?
Solution
The Johnson–Neyman technique improves upon the traditional simple slopes approach by identifying the precise regions of the moderator variable where the effect of the predictor is statistically significant. Instead of testing arbitrary low, medium, or high values, it provides a continuous range that shows where the predictor’s effect transitions from nonsignificant to significant, giving a clearer and more accurate picture of the conditional relationship.
And some more questions from the tutors:
- What is the advantage of conducting moderation analysis using regression analysis rather than 2x2 ANOVA?
Solution
Regression analysis is ultimately much more general and versatile because a regression approach does not require that the two variables being crossed be categorical. They can be categorical, continuous, or any combination of categorical and continuous.
- Take a look at Table 2 (Simple effects): If we consider the interaction effect significant and both variables would not be the reference category, the feeling towards immigrants would then be calculated as 51.545+12.555=64.1. Is that correct?
Solution
No, as it is calculated by adding both coefficients from main effects + the interaction effect (51.545–4.446–4.535+12.555=55.119), but remember that the main effects are not significant
- Take a look at the table 2 again: If we consider the borderline p-value of 0.11 for XxW to be significant, as the authors do, but the main effects are not significant, can we still interpret the interaction effect?
Solution
Lack of significant main effects does not prevent interpreting a significant interaction. Interactions test a different hypothesis (that the effect of X depends on W), and it’s common to see meaningful interactions with null main effects.
Proper way to proceed:
- Interpret simple effects (e.g., effect of X at specific levels of W, and vice-versa).
- Show an interaction plot and report CIs/effect sizes, not just p-values.
- Consider Johnson–Neyman intervals (for continuous W).
- Keep all lower-order terms in the model (hierarchical principle) and note the limited evidence (p=0.11).
7.15 Quiz
| True | False | Statement |
|---|---|---|
| Moderation analysis can be conducted by adding an interaction term in a regression analysis. | ||
| Moderation occurs when a third variable (Z) affects the relation between an independent variable (X) and the dependent variable (Y). | ||
| The simple (conditional) effect is the effect of X (or Z) on Y when Z (or X) is equal to 0. | ||
| Standardization of the variables is useful to mitigate multicollinearity. |
7.16 Time to practice on your own
You can download the PDF of the exercises here:
In this exercise, we will use the data “protest.sav” (Hayes, 2022) which can be downloaded 
or here under “data files and code”. Especially, we will focus on the following variables:
- Protest (independent variable): A lawyer protests against gender discrimination (experimental group, dichotomous 0 = no and 1 = yes)
- Like (dependent variable): assessment of the lawyer (scale 1-7)
- Sexism (moderator): perception of sexism as a ubiquitous problem in society (scale 1-7)
7.16.1 Exercise 1: protest with a continuous moderator
We want to test the assumption that when women believe that sexism is a problem in society, they like the lawyer more when he protests sexism than when he doesn’t protest.
Start by drawing the regression equations.
Solution: equation
The regression equation go as:
\[ Y_i = \beta_0 + \beta_1*Protest_i + \beta_2*Sexismus_i + \beta_3*(Protest*Sexismus_i) + \epsilon \]
Now, we want to know if the overall model is significant? Start by importing the data:
Note that there are several ways to center the variables when creating the interaction term.
Show the code
# interaction term
# without centering
db$ProtestXSexism1 = db$protest*db$sexism
# with centering
db$ProtestXSexism2 = (db$protest-mean(db$protest)) * (db$sexism-mean(db$sexism))
# z-standardization
# db$ProtestXSexism3 = scale(db$protest)*scale(db$sexism)
# view
head(db)
## sexism liking respappr protest x Sexism_h_t ProtestXSexism1 ProtestXSexism2
## 1 4.25 4.50 5.75 0 4 1 0 0.5914260
## 2 4.62 6.83 5.75 0 6 1 0 0.3390229
## 3 4.62 4.83 5.25 0 4 1 0 0.3390229
## 4 4.37 4.83 4.25 0 5 1 0 0.5095655
## 5 4.25 5.50 2.50 0 3 1 0 0.5914260
## 6 4.00 6.83 4.75 0 3 1 0 0.7619686Now, run the regression model:
Show the code
# regression model (with centering)
m.cent = lm(liking ~ protest + sexism + ProtestXSexism2, data=db)
summary(m.cent)
##
## Call:
## lm(formula = liking ~ protest + sexism + ProtestXSexism2, data = db)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.9894 -0.6381 0.0478 0.7404 2.3650
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.79659 0.58679 8.174 2.83e-13 ***
## protest 0.49262 0.18722 2.631 0.00958 **
## sexism 0.09613 0.11169 0.861 0.39102
## ProtestXSexism2 0.83355 0.24356 3.422 0.00084 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9888 on 125 degrees of freedom
## Multiple R-squared: 0.1335, Adjusted R-squared: 0.1127
## F-statistic: 6.419 on 3 and 125 DF, p-value: 0.0004439
# regression model (without centering)
m.roh = lm(liking ~ protest + sexism + ProtestXSexism1, data=db)
summary(m.roh)
##
## Call:
## lm(formula = liking ~ protest + sexism + ProtestXSexism1, data = db)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.9894 -0.6381 0.0478 0.7404 2.3650
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.7062 1.0449 7.375 1.99e-11 ***
## protest -3.7727 1.2541 -3.008 0.00318 **
## sexism -0.4725 0.2038 -2.318 0.02205 *
## ProtestXSexism1 0.8336 0.2436 3.422 0.00084 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9888 on 125 degrees of freedom
## Multiple R-squared: 0.1335, Adjusted R-squared: 0.1127
## F-statistic: 6.419 on 3 and 125 DF, p-value: 0.0004439How much variance does the model explain? Are there main effects or conditional effects? If yes, what do they look like?
Solution: interpretation
The overall model is significant (p < .001) and explains 13.3% of the variance. We are allowed to interpret the results of the regression.
There is a significant conditional effect of protest when sexism = 0. It is not a main effect since interaction is also included.
Protest has an effect on the assessment if the moderator (sexism) has the value zero (= a medium level, since mean centered)
Is there a moderation effect?
Show the code
# run the model without the interaction term
m0 = lm(liking ~ protest + sexism, data=db)
# compare the R2
summary(m.cent)$r.squared - summary(m0)$r.squared
## [1] 0.08119242
# get EtaSq
DescTools::EtaSq(m.cent)
## eta.sq eta.sq.part
## protest 0.047991546 0.052478399
## sexism 0.005136019 0.005892326
## ProtestXSexism2 0.081192415 0.085672955If so, how much variance does this explain and what does this effect mean in general?
Solution: interpretation
The interaction of protest and sexism perception is significant. There is a moderation effect.
The effect of the protest on the lawyer’s assessment varies depending on how strongly the subjects perceive sexism as a problem.
The interaction contributes 8.1% to explaining the variance. The dependent variable is thus better explained if moderation is taken into account.
Main effects are conditional effects when an interaction is present. After centering, you are testing the effect of each predictor at the mean of the other. So, the nonsignificant sexism coefficient simply means: Among participants at an average level of sexism belief, and when the lawyer does not protest, sexism does not significantly predict liking. That does not contradict the significant interaction — it just says the average effect is not strong on its own. So, the loss of significance after centering does not mean sexism stopped mattering. It means the interpretation of the coefficient changed: from an artificial reference (sexism = 0) to a meaningful one (sexism = average).
Illustrate the moderation effect graphically and interpret it. First, we can create an interaction plot:
Show the code
# extract the needed coefficients
intercept.p0 = coefficients(m.roh)[1]
intercept.p1 = coefficients(m.roh)[1] + coefficients(m.roh)[2]
slope.p0 = coefficients(m.roh)[3]
slope.p1 = coefficients(m.roh)[3] + coefficients(m.roh)[4]
# interaction plot
par(mfrow=c(1,1))
farben = c("red","blue")
plot(db$sexism, db$liking, main="Interaction",
col=farben[db$protest+1],pch=16,
xlab="Sexism",ylab="Liking")
abline(intercept.p0,slope.p0,col="red")
abline(intercept.p1,slope.p1,col="blue")
legend("bottomleft",
c("Protest=0","Protest=1"),
col=c("red","blue"),pch=16)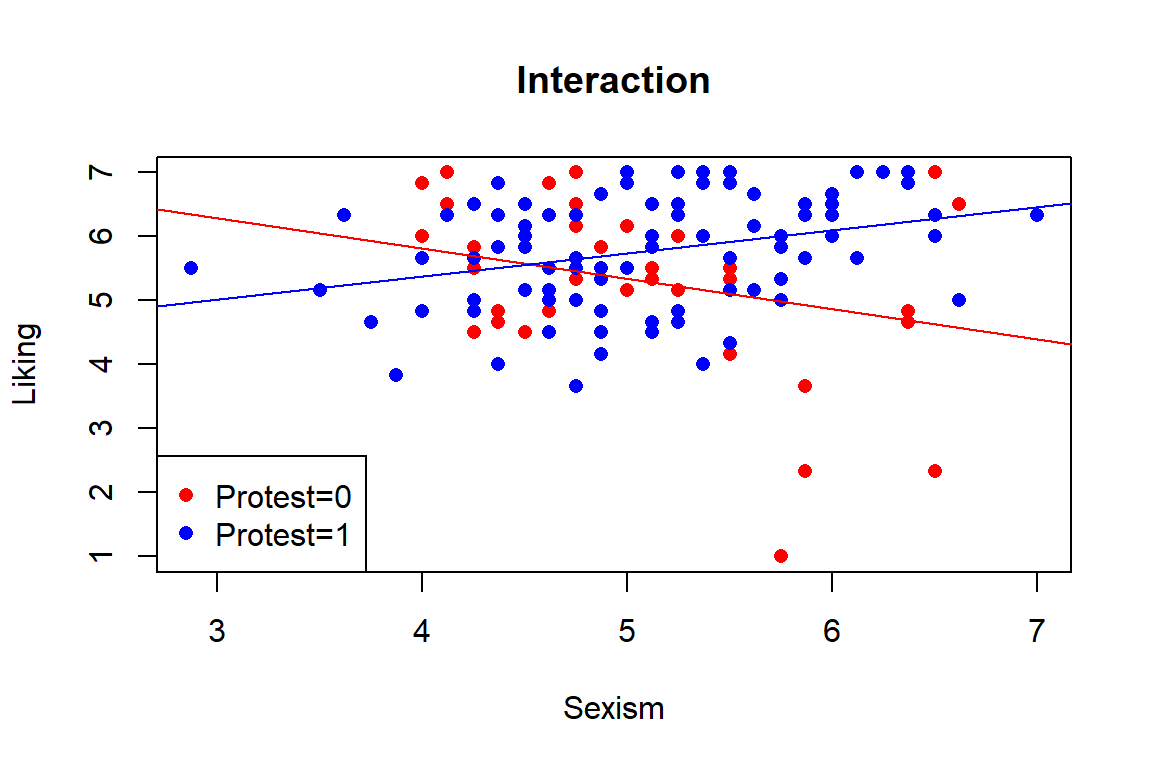
Solution: interpretation
The code is computing the simple regression lines (simple intercepts and slopes) for each level of the binary moderator protest (0 vs 1) from the uncentered model m.roh:
\[ liking = \beta_0 + \beta_1(protest) + \beta_2(sexism) + \beta_3(protest * sexism) \] With protest coded 0/1, for protest = 0:
\[ liking = \beta_0 + \beta_2(sexism) \] \[ intercept.p0 = \beta_0 \] (line’s value at sexism = 0) \[ slope.p0 = \beta_2 \] (effect of sexism when protest = 0)
For protest = 1:
\[ liking = (\beta_0 + \beta_1) + (\beta_2 + \beta_3)sexism \] \[ intercept.p1 = \beta_0 + \beta_1 \] (baseline shift when protest = 1) \[ slope.p1 = \beta_2 + \beta_3 \] (effect of sexism when protest = 1)
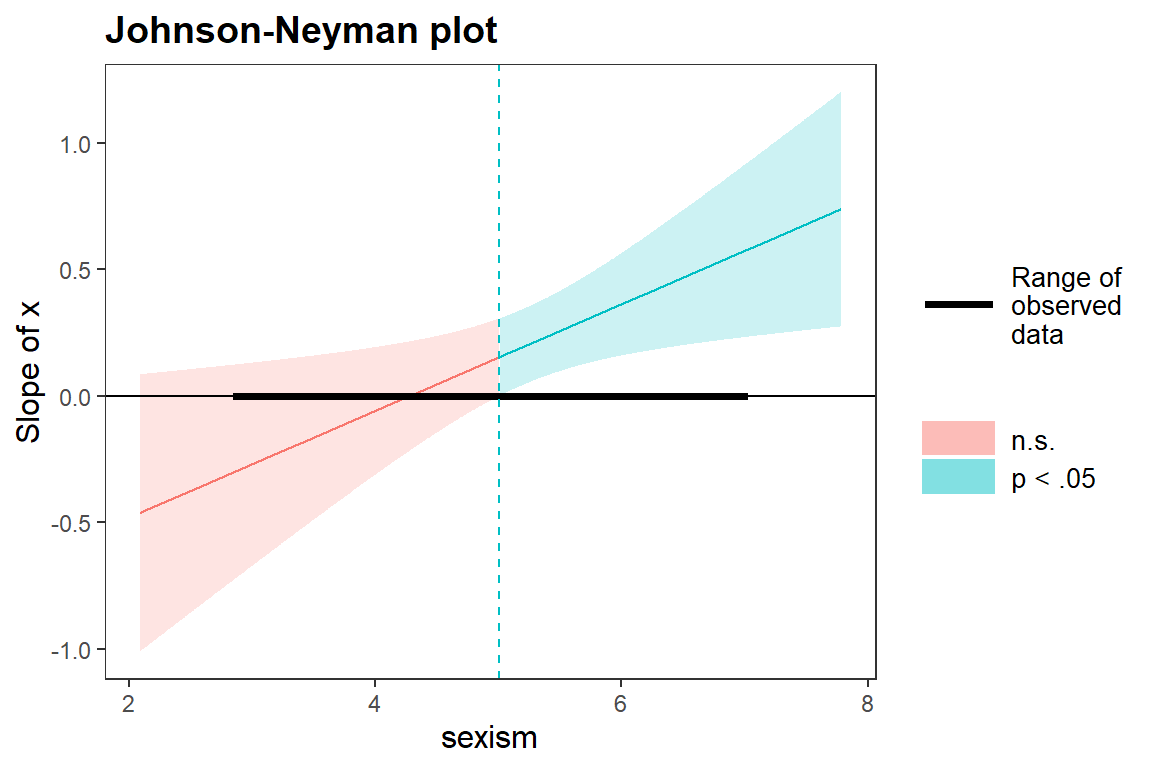
Second, we can provide a Johnson-Neyman plot:
Show the code
library(interactions)
m.simplified = lm(liking ~ protest*sexism, data=db)
johnson_neyman(m.simplified,"protest","sexism")
## JOHNSON-NEYMAN INTERVAL
##
## When sexism is OUTSIDE the interval [3.51, 4.98], the slope of protest is p < .05.
##
## Note: The range of observed values of sexism is [2.87, 7.00]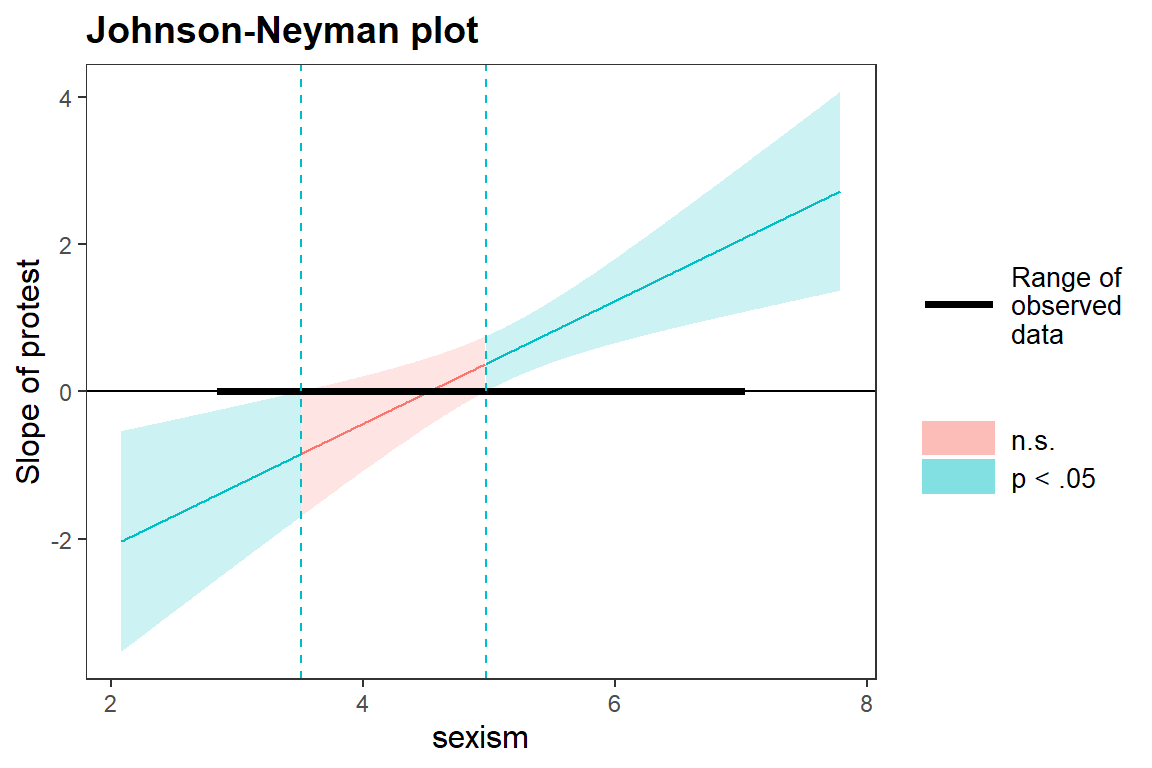
Solution: interpretation
The Johnson–Neyman plot illustrates how the relationship between sexism and protest changes depending on the level of sexism. The horizontal black bar indicates the observed range of the data.
- The red shaded area marks the region where the slope of protest is not statistically significant (p > .05). This means that for middle range levels of sexism (approximately between 3.5 and 5 on the scale), the effect of sexism on protest is not reliably different from zero.
- The blue shaded areas indicate regions where the slope is statistically significant (p < .05). At lower levels of sexism (< 3.5), the slope is significantly negative: higher sexism predicts less protest. At higher levels of sexism (> 5), the slope is significantly positive: higher sexism predicts more protest.
- This pattern suggests a crossover interaction: the effect of sexism on protest depends strongly on where individuals fall on the sexism scale.
In short, sexism has no clear effect in the middle of the scale, but is negatively related to protest among individuals low in sexism, and positively related to protest among individuals high in sexism.
7.16.2 Exercise 2: protest with a dichotomous moderator
Now, divide the moderator into a dichotomous variable (sexism low vs. high) with a median split and recalculate the moderation analysis.
Show the code
# Median split
db$sexism.ms = as.integer(db$sexism>=median(db$sexism))What changes in the output?
Show the code
# new model
m3 = lm(liking ~ protest*sexism.ms, data=db)
summary(m3)
##
## Call:
## lm(formula = liking ~ protest * sexism.ms, data = db)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.9179 -0.6815 0.1263 0.7963 2.0821
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.6491 0.2125 26.584 < 2e-16 ***
## protest -0.1154 0.2634 -0.438 0.66199
## sexism.ms -0.7312 0.3122 -2.342 0.02074 *
## protest:sexism.ms 1.2090 0.3779 3.199 0.00175 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9967 on 125 degrees of freedom
## Multiple R-squared: 0.1195, Adjusted R-squared: 0.09839
## F-statistic: 5.656 on 3 and 125 DF, p-value: 0.001148
# get EtaSq
DescTools::EtaSq(m3)
## eta.sq eta.sq.part
## protest 0.043987025 0.047581194
## sexism.ms 0.002000014 0.002266368
## protest:sexism.ms 0.072096985 0.075686621
# get the coeff
meanvalues = tapply(db$liking, list(db$protest,db$sexism.ms),FUN=mean)
meanvalues
## 0 1
## 0 5.649091 4.917895
## 1 5.533659 6.011489
Solution: interpretation
R-square significantly worse (probably due to loss of information during dichotomization) and the coefficients change slightly.
There are only two Simple Slopes because there are only two moderator levels. There are no Johnson-Neyman values.
Calculate the moderation analysis again with the variable «x» as the independent variable (it measure the lawyer protests to varying degrees on a scale of 1-7) and the metric moderator. What changes in the output?
Show the code
# new model
m4 = lm(liking ~ x*sexism, data=db)
summary(m4)
##
## Call:
## lm(formula = liking ~ x * sexism, data = db)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.0451 -0.6128 0.1029 0.7720 1.6583
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 8.65856 1.90366 4.548 0.0000126 ***
## x -0.90210 0.45129 -1.999 0.0478 *
## sexism -0.73604 0.36256 -2.030 0.0445 *
## x:sexism 0.21069 0.08563 2.460 0.0152 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.009 on 125 degrees of freedom
## Multiple R-squared: 0.09858, Adjusted R-squared: 0.07695
## F-statistic: 4.557 on 3 and 125 DF, p-value: 0.004584
# get EtaSq
DescTools::EtaSq(m4)
## eta.sq eta.sq.part
## x 0.046574596 0.04912969
## sexism 0.006844541 0.00753586
## x:sexism 0.043654300 0.04619148
Solution: interpretation
Now the hypothesis is that the more women believe that sexism is a problem, the more they like the lawyer, the more she protests.
The coefficients change, the explanation of variance overall and through the interaction alone is weaker in each case (but this is simply because it is a completely different and only a simulated variable).
What changes in the graphics?
Show the code
# plots
johnson_neyman(m4,"x","sexism")
## JOHNSON-NEYMAN INTERVAL
##
## When sexism is OUTSIDE the interval [0.20, 5.01], the slope of x is p < .05.
##
## Note: The range of observed values of sexism is [2.87, 7.00]